Compared to the long histories of other musical instruments, the history of the piano is relatively short. Invented only 250 years ago, its design had evolved and improved constantly since then. By using an increasingly more complex system of levers and springs, piano technicians have fine-tuned the reliability, musicality, and feel of the piano action (the 88 key mechanisms) to a point where few, if any changes, have been needed to the action for the past century.
During the past decade, however, the development of electronic pianos and synthesizers have created a need for new study into the area of piano actions. Because of the high cost and size of the key mechanism, engineers cannot put actual piano actions into electronic pianos and synthesizers. Instead, they have tried to use simple spring mechanisms and miniature piano hammers to imitate the feel of a real piano action in these devices. Unfortunately, their attempts so far have generally been considered inadequate. Piano teachers universally feel that all except the most amateur of students should learn on real pianos.
The piano actions in electronic pianos must be radically redesigned if they are to more closely imitate those of real pianos. This type of change requires that piano technicians abandon the traditional view of piano making as some sort of sacred art. The workings of the piano action must be quantified first if it is to be imitated with any degree of accuracy. In this report, a mathematical model of a piano key action is developed and recommendations for possible new piano designs are made based on findings from the model.
To understand how a piano action works, one must first understand what a piano action does. This requires a basic understanding of how sound is created inside a piano.
Sound is merely the vibration of air. People's ears are able to detect this vibration and interpret it as sound. The sound of a piano note comes from vibrating metal wires inside the piano. The vibrations of these "piano strings" cause a giant wooden board at the back of the piano, known as a sound board, to also vibrate. This sound board amplifies the tiny vibrations of the strings enough that people can hear it.
Through a system of levers, the pressing of a piano key causes a felt hammer to hit the strings with tremendous speed. This causes the strings to vibrate. Once the hammer has hit the strings, it is prevented from touching the strings again, as this will kill the vibrations; however, in order to give the pianist control of when the vibrations will end, the piano key is connected through another system of levers to a felt block called a damper. When a piano key is released, the damper falls onto the strings and stops their vibrations. As long as the piano key is released, the damper will stay in contact with the string to prevent the vibration of other strings from inducing unwanted vibrations in that string. When the piano key is pressed, the damper will lift off from the string just before the hammer strikes the string starting a vibration, and remains off until the key is once again released.
A piano action is made up of a complicated system of levers and springs. The interactions between the various parts can best be understood by examining each part in isolation from the others.
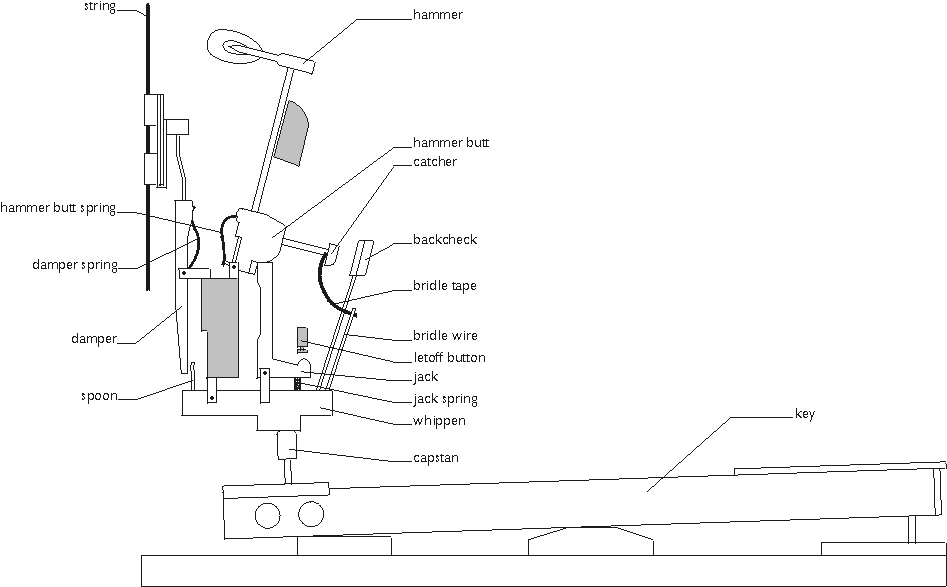
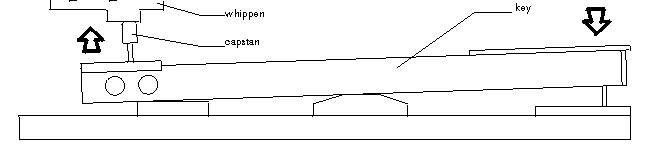
Although only a few inches of a piano key can be seen from the outside, it actually extends deep into the piano. It is merely a simple lever which when pressed down on one side by a pianist, pushes up on the other side against the whippen, another lever. Since each key of a piano is of a different size, weights are often added so as to give all the keys a consistent weight. Various adjustments can be made to the key to change its angle or the depth to which it can be depressed.
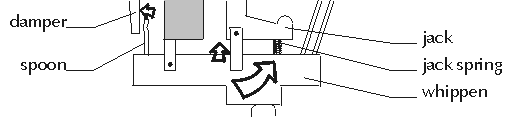
The piano key actually moves a very small amount when pressed. As a result, a second lever, the whippen, is needed to provide additional leverage thereby increasing the amount of movement. When the capstan pushes up against the whippen, it pushes the jack upwards against the hammer and pushes the spoon towards the damper.
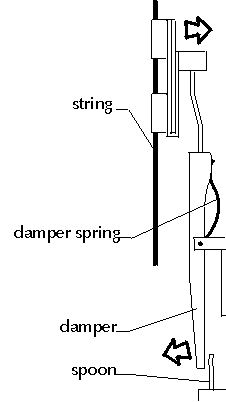
The damper is held tightly against the piano string by a strong spring. When the piano key is pressed, the spoon on the whippen lifts the damper off of the string.
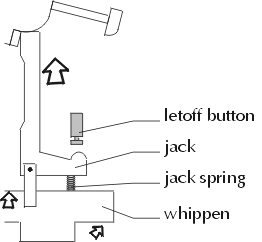
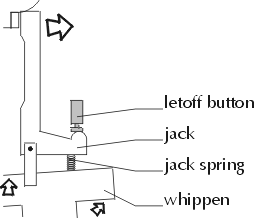
The jack plays a very important role in the piano action. When the whippen pushes up against the jack, the jack initially pushes up against the hammer. As the jack moves higher and higher, part of the jack makes contact with the letoff button. If the whippen continues to push up against the jack, the jack will move outwards instead of upwards. This outwards movement causes it to fall out from beneath the hammer. The reason for this is explained in the hammer section.
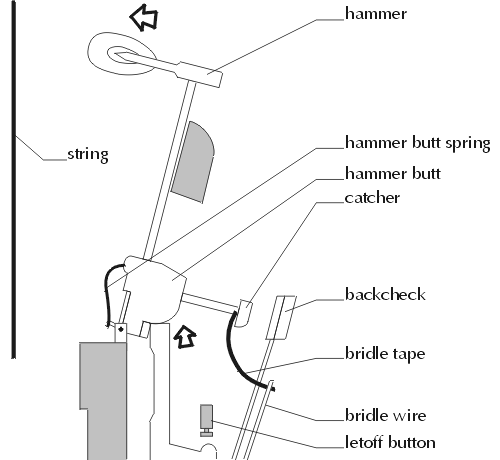
The movement of the hammer must satisfy 3 requirements: it must hit the string with tremendous force; after is has hit the string, it must fall away so as to let the string vibrate; and if the note is played repeatedly, it must hit the string consistently each time. When the piano key is initially pressed, it causes the whippen to move upwards. This motion is converyed directly to the hammer through the jack. Because the hammer is, in fact, a lever, the small movement of the jack is multiplied causing the hammer to move a great distance at great speed.
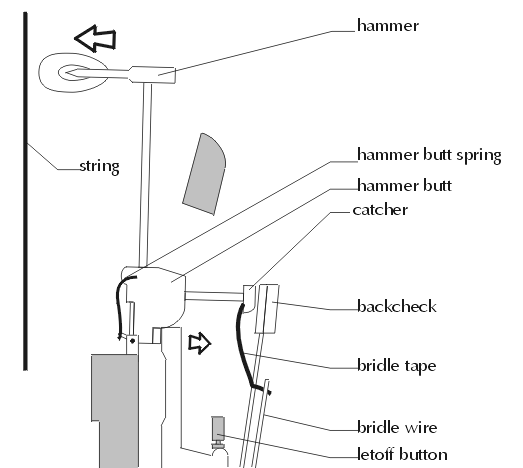
As the jack pushes up against the hammer, it eventually makes contact with the letoff button. This causes the jack to move outwards instead of upwards; the jack no longer pushes up against the hammer. Even though the hammer hasn't yet made contact with the string at this point, it has enough momentum to reach it.
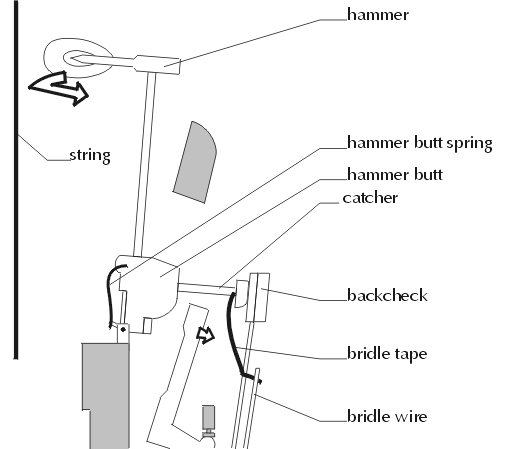
After it has hit the string, it rebounds backwards and is caught by the backcheck. The back check is important because without it, the hammer would fall too far, and the jack would be unable to return to its position underneath the hammer when the key is released. The hammer butt spring and bridle tape (a leather strap) are needed because when the key is released and the backcheck falls away, the hammer falls back downwards very slowly. They help push the hammer down more quickly.
Two factors are important in determining the feel of a piano action: the amount of force needed to keep the key stationary and the amount of force needed to accelerate the key by a certain fixed amount. An accurate mathematical model of a piano action must incorporate both of these factors. Although both factors are related, each is independent of the other. As a result, each can be examined separately.
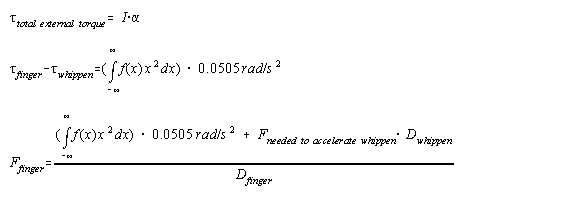
When the piano action is stationary, it is considered to be in a state of equilibrium. The amount of force being applied by the pianist to the key is equal to the gravitational forces and elastic forces acting inside the system. Since all of the piano parts rotate around various pivots, standard torque equations can be used in developing the mathematical model.
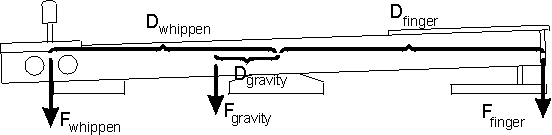
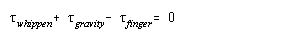
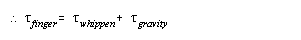
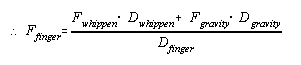
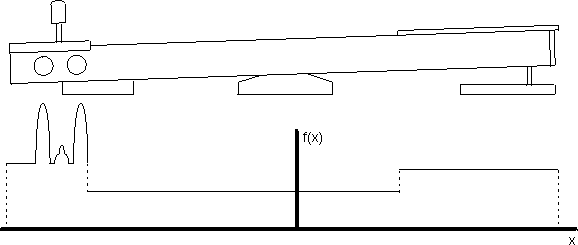
Figure 10 shows a simple diagram of the forces acting on a piano key, and figure 11 expresses the relationship between those forces as an equation. Since the force being exerted by the finger prevents the key from moving, it must be equal to the force of gravity and the downwards force of the whippen. The force of the finger is the unknown being searched for. The force of the whippen can be determined by doing a similar analysis of the forces acting on the whippen as is being done here. And the total force of gravity is known, but the position of the force in unknown. In torque calculations, the force of gravity is considered to act on the system's center of mass. To calculate the center of mass, calculus must be used. Figure 12 shows a key and its equivalent graphical representation. The distance from the pivot is plotted on the x-axis and the product of the cross-sectional area of the key and the density of the wood is plotted on the y-axis. Then, by solving the equation in figure 13, one can find the center of mass for the key. This being done, the equation can be solved. Similar calculations can be done on the other parts of the piano though springs and other moving parts that exert differing amounts of forces depending on how far the key has been pressed add additional complications. Once these calculations have been done, the results can be combined together to give the series of equations shown in figure 14. The variable k is the distance in cm that the key is pushed down. The result is in (g)(cm)/s2. Note how the amount of force required varies depending on how far the key is depressed.
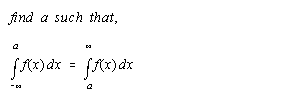
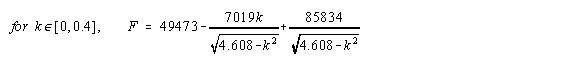
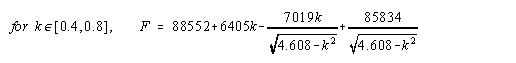
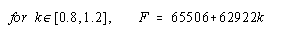
Though the equilibrium calculations provide much insight into the feel of the piano action, they alone cannot fully describe the piano action. They do not take into the account how the mass and shape of each part affects its acceleration and momentum. The acceleration calculations are needed to incorporate these ideas into the model. These equations try to determine the amount of force needed to accelerate the end of the key by 1 cm/s2. On the piano used for the measurements, this was equivalent to an angular acceleration of 0.0505 radians/s2 (some pianos may have different key lengths, resulting in different values). Then, by solving the equation in figure 15, one arrives at the result in figure 16: the amount of force needed to accelerate the key and other parts of the action.


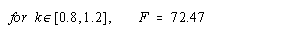
Together, the equilibrium and acceleration equations accurately describe the feel of a piano action. These two sets of equations are expressed graphically in figures 17 and 18. The two graphs clearly reveal three distinct stages in the action. By emulating the mathematical model represented by these two graphs, a very accurate piano action imitation can be made.
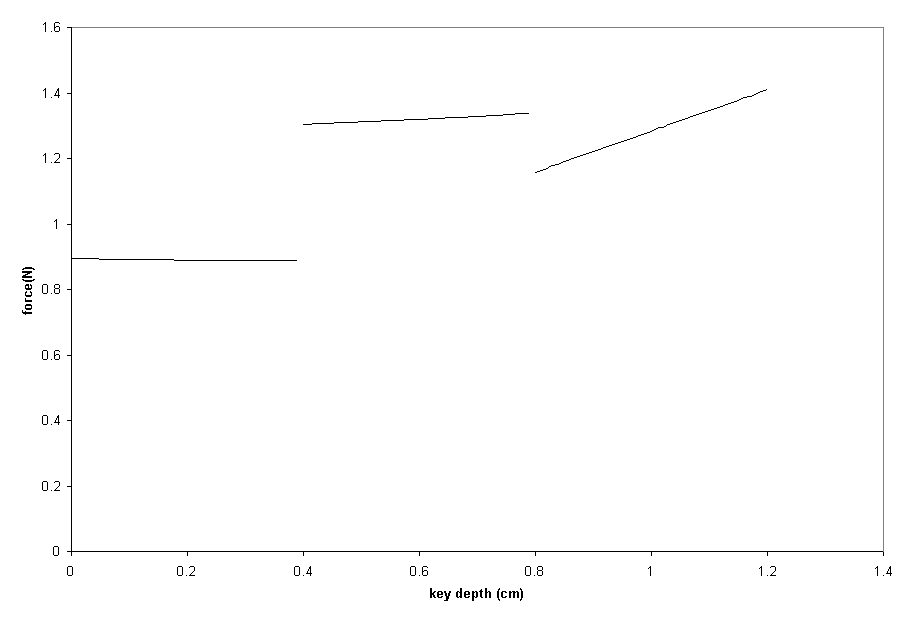
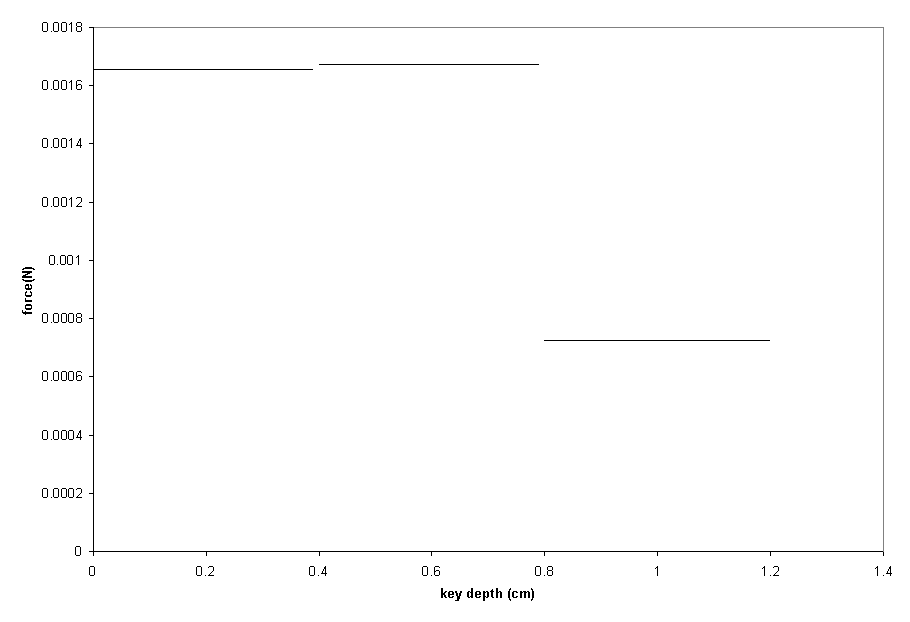
A piano action is a very complex system. An action must have three different stages if it is to feel similar to that of a real piano action: an initial stage, a main stage, and a follow-through stage. During the initial stage, the whippen spoon is not pushing against the damper. Consequently, the key is easy to push down. As the key is pressed down further, the main stage is entered. During this stage, the damper is pushed by the whippen spoon, so the amount of force needed to press the key is much higher. Finally, during the follow-through stage, the jack touches the letoff button and moves away from the hammer. Since the jack no longer pushes up against the hammer, the force needed to move the key lessens considerably.
To accurately imitate a real piano action, an imitation piano action must contain these three stages. Each stage is so significantly different from the others that even a crude representation of these stages will result in a good likeness of a real piano action. Imitation actions based on simple spring mechanisms are too simplistic to provide a good feel, yet those based on miniature piano actions, though providing good accuracy, are far more complex than necessary. A possible compromise of accuracy and complexity probably exists between these two extremes.
Ming April 18, 2002: Actually, all of these applications are pretty bogus. In retrospect, the ideas listed here either don't work or aren't practical. I've kept the stuff here for completeness though.
This model can be used immediately in comparing the accuracy of various electronic piano actions. By applying a similar analysis to those actions, a mathematical model of the action can be created which can then be compared with the mathematical model of a real piano action. The model can also be used in makeing adjustments of the shapes, weights, and materials of the various parts so as to more closely adhere to the model.
The model also suggests possible new design for electronic piano actions. One possibility is displayed in figure 19. It contains the three stages that are required of a good imitation action and with some minor adjustment can be made to adhere to the model very precisely. The spring underneath the key is used to imitate the extra force needed to move the damper in the main stage. When the key is pressed down far enough, the second lever falls off of the first lever and presses up against the side of the first lever. This results in the reduction of force necessary to imitate the follow-through stage.
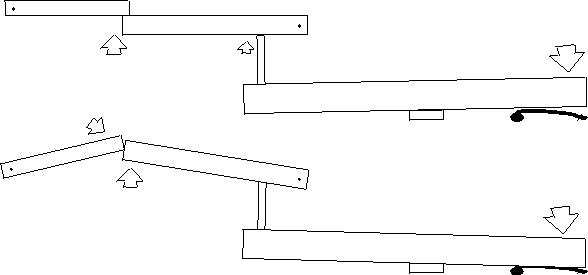
The model can also be used in improving the design of traditional piano actions. Presently, technicians determine the force needed to push down on a key by placing differing weights on the end of a key and observing how much the key moves. This process is inaccurate and produces very subjective results. Instead of this error-prone process, piano technicians and engineers could use the mathematical modelling techniques used here to determine a much more accurate figure. This improved accuracy enables designers to more accurately balance the weights of all the keys on the piano, and it also provides a means for comparing the feel of actions from different piano manufacturers.
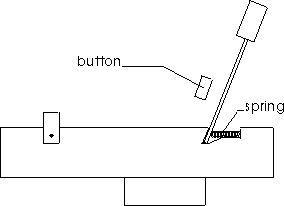
The modelling of a piano action also encourages piano technicians to develop a deeper understanding of the interactions of the various parts in a piano action. This could perhaps foster new improvements to the traditional action design which has not changed significantly over the past century. For example, the addition of a spring to the back check, as shown is figure 20, could help improve the repetition speed of upright piano actions. When the key is pressed and the whippen moves, the back check presses up against the button and is pushed backwards. When the key is released and the whippen falls back down, the spring keeps the back check pressed against the button ensuring that the hammer is in the optimum position for allowing the jack to fall back under it. This results in better repetition.
The quantification of a piano action, though time-consuming, involves only some basic knowledge of high school calculus and high school physics. The resulting model provides valuable insight into the design of piano actions. These insights can provide the guidance necessary to greatly improve the accuracy and cost of future piano action designs.
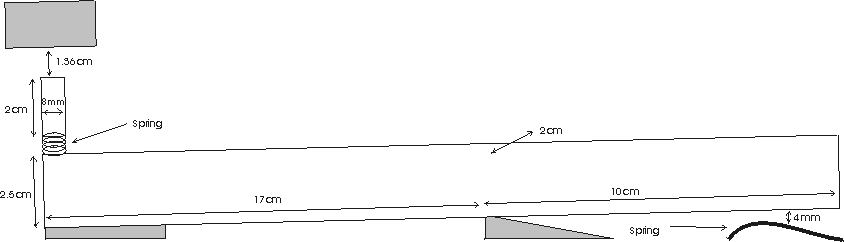
Ming April 18,2002: After talking to Mr. Stanwood for a bit, I started thinking about piano key actions again, and I realized that it might be possible to build a piano action that could imitate a standard piano action fairly well without requiring a full jack. By taking a wooden key and attaching a lead weight on the end using a spring, one can emulate the sudden decrease in acceleration force caused by the jack lifting off by pressing this weight against another object. The feel of the damper can be emulated by another spring under the key. The springs have to be chosen carefully so as to imitate the springs in a real piano key.

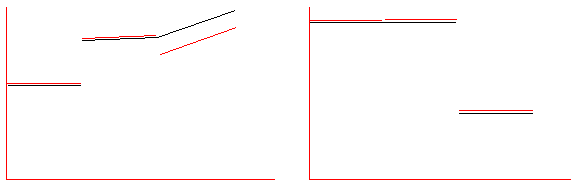
I believe the equilibrium and acceleration graphs for this key will be pretty close to that of a realy piano key. Below I have graphs showing the results for a real key (in red) and the new key (in black). They match well except for when the jack "lifts off" in the equilibrium graph.
I haven't gotten around to building this and seeing how good it feels. It shouldn't be too hard to do though. I'm not sure how well this compares to existing artificial piano actions or whether this has already been done or not. It is sort of interesting though.
"How to Build Balsa Bridges." Internet: http://www.borg.com/~freitag/idea.htm.
"Periodic Table." Internet: http://140.198.18.108/periodic/Pb.html.
Asminov, Isaac. Understanding Physics. Dorset: Dorset Press, 1966.
Fine, Larry. The Piano Book: Buying and Owning a New or Used Piano. 2nd ed. Boston: Brookside Press, 1990.
Harding, Rosamond. The Piano Forte:Its History Traced to the Great Exhibition of 1851. London: Cambridge University Press, 1933.
Howe, Alfred. Scientific Piano Tuning and Servicing. Mount Vernon: Press of A. Colish, 1955.
McCombie, Ian. The Piano Handbook. New York: Charles Scribner's Sons, 1980.
Reblitz, Arthur. Piano Servicing, Tuning, and Rebuilding. New York: The Vestal Press, 1976,
Tilley, Donald. Contemporary College Physics. Menlo Park: The Benjamin / Cummings Publishing Company, Inc., 1979.
Wolfenden, Samual. A Treatise on the Art of Pianoforte Construction. London: Unwin Brothers, Ltd., 1916.
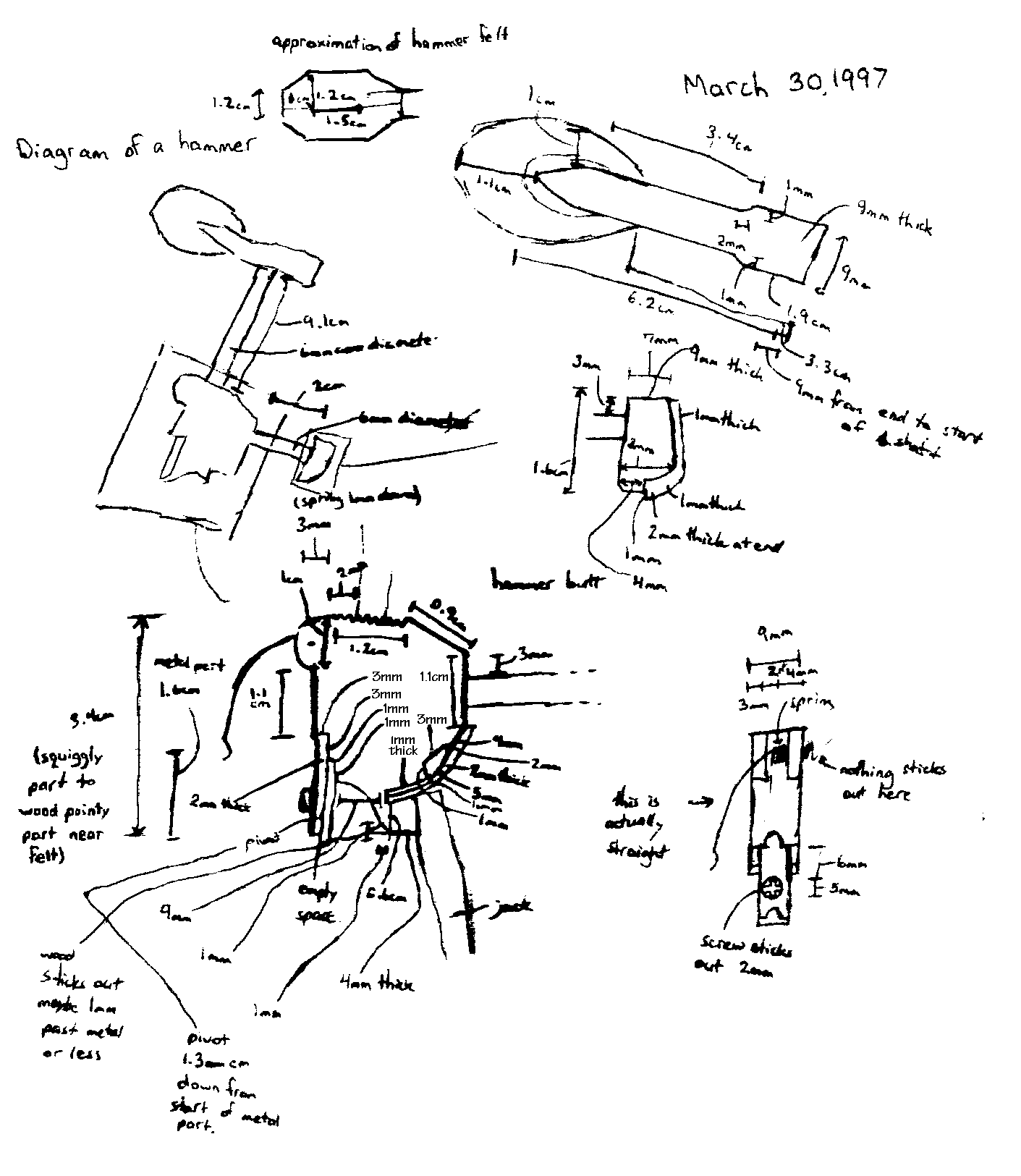
In the original report, some 70 pages of research notes appear here. They include diagrams, measurements, discussions of techniques used, calculations, a list of assumptions, and other things. Unfortunately, these notes are too large to include here. Instead, a scan of one of the pages of research notes (modified slightly to improve readability) is included here as a stand-in for what was there.